




 |
 |
 |
 | 25 GnuPG and the mystery of large numbers
| Contents |
 |
Cryptography for non-mathematicians
There have been several attempts at 'cracking' the RSA algorithm
on which GnuPG is based5, i.e. to
calculate a private key when only the public key is known. However,
this type of calculation has never been successful for the key lengths
(1024 Bit and above) that are used in GnuPG. While it might be
possible on a theoretical level, it is practically impossible since
even with plenty of time (many years) and thousands of networked
computers, there would never by sufficient storage to complete the
last steps of this calculation.
At the same time, it is entirely possible that one day an ingenious mathemtatical idea will provide a solution to the mathematical issues behind RSA. However, this is unlikely to happen anytime soon.
From time to time the German Federal Agency for Security in Information Technology (BSI) publishes forecasts and assessments with regards to how long certain key lengths can likely be used for absolute security guarantee. GnuPG's standard settings far exceed these minimum requirements. As touched upon in the previous chapter, the mathemetical elements form by far the most secure portion of practically applied cryptography.
The following discussion will show you how this mathematical method works. While not all details will be covered - as this would be far beyond the scope of this manual - with some effort on your part it will enable you to make correct en/decryption calculations and thus discover the "mystery of big numbers".
Even non-mathematicians and mortals can understand this complex mathematical method. All that is required is a good grasp of simple additions and multiplication processes. It may be compared to the concept of a free skate, because the free skate is really much more about substance than the short program which is much heavier on the required elements. But most importantly, it will help you to understand why GnuPG is so secure.
But first let us get some terminology out of the way:
Arithmetics is the method by which numbers are added and multiplied.
Encryption using GnuPG is based on the so-called RSA algorithm6. RSA is derived from the last names of Ron Rivest, Ami Shamir und Ben Adleman, who discovered this algorithm in 1978. This algorithm uses a type of arithmetic which is called arithmetic with residue classes or "modular (or modulo) arithmetic" .
Calculating with residue classes means only calculating the "residue" (or remainder) which remains after an integer division by a whole number. This number, by which the division is carried out, is called the "module" or "modular number". If we calculate with the factor or the modular number 5, for example, this is called "arithmetic modulo 5".
For in allustration of how arithmetic with residue classes - also called modular or congruence arithmetic - works, imagine the face of a clock:
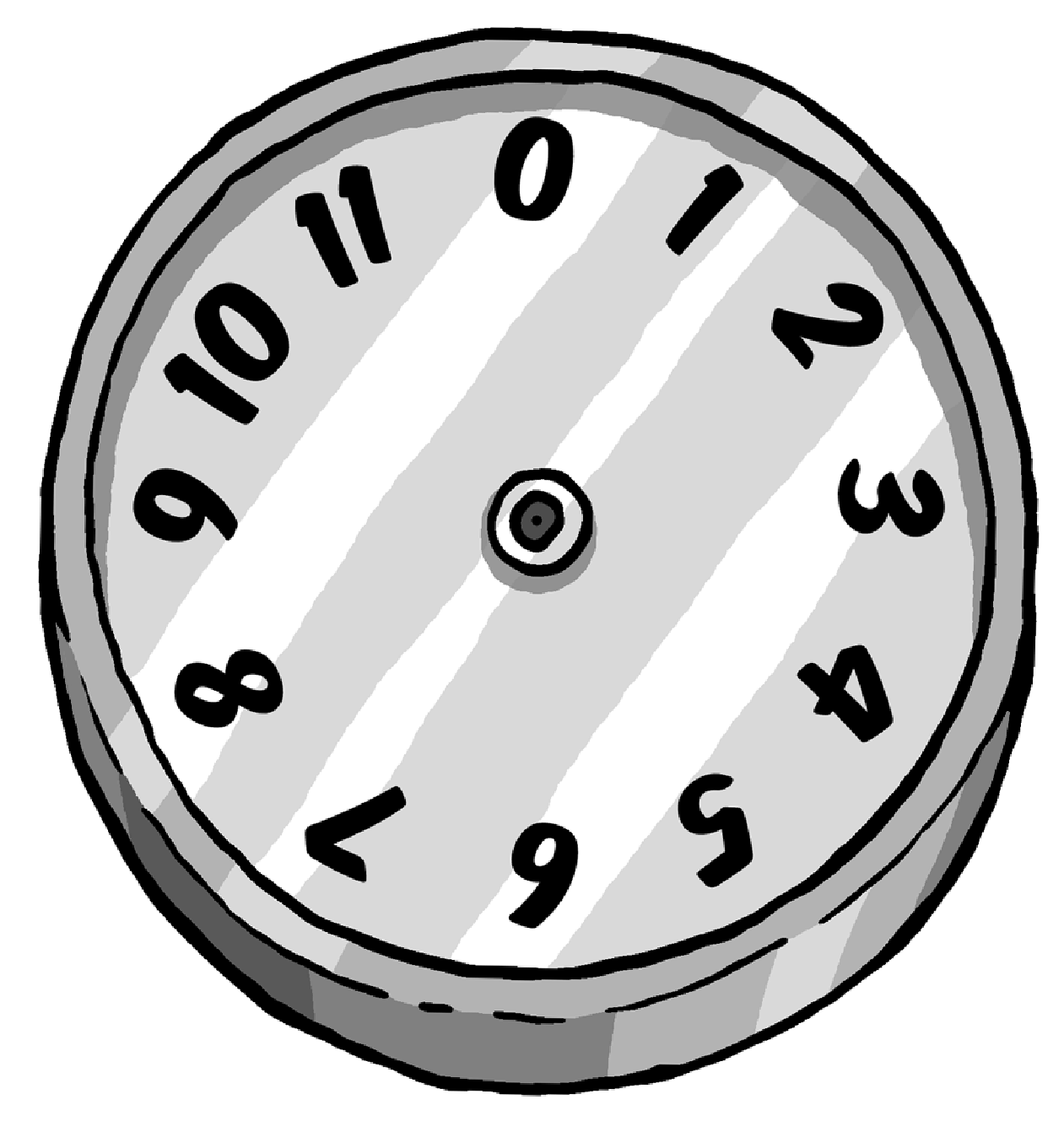
This clock is an example of arithmetic modulo 12 (hence the factor is also 12) -- a clock with an ordinary dial, except that it has a 0 where one would expect to see the 12. Using this example we can describe modulo arithmetic by simply moving the imaginary dial.
For example, to calculate 3 + 2, we begin at digit 2 and turn the dial by three digits (or start at 3 and turn by two digits, which works out to the same). The result is 5.
Using the same method to add 7 + 8, the result is 3. Why? 3 is the residual that results when dividing 15 (i.e. 7 + 8) by 12. To multiply 5 by 7, start at 0 and move forward by 5 digits each time for seven times (or begin by 0 and move forward by 7 digits 5 times). In both cases the dial stops at 11 because 11 is the residual obtained from dividing 35 (i.e.7 * 5) by 12.
Therefore, by using arithmetic with residue classes we add and divide numbers according to the conventional rules of everyday arithmetics, while always only using the residual that remains after the division. The modulus (the factor) is added to indicate that the rules of modular arithmetic rather than conventional arithmetic are applied, hence we would say, for example, "4 modulo 5", or in short "4 mod5".
A modulo 5 for example would be represented by a clock with only 5 numbers (0, 1, 2, 3, 4), hence:
4 mod5 + 3 mod5 = 7 mod5 = 2 mod5
Said another way, using arithmetic modulo 5 the result of adding 4 and
3 would be 2.
Another example of modulo 5 arithmetics:
8 mod5 + 6 mod5 = 14 mod5 = 4 mod5
You can see that it doesn't matter in which sequence you proceed, because you could also write:
8 mod5 + 6 mod5 = 3 mod5 + 1 mod5 = 4 mod5
3 is the same as 8, and 1 the same as 6, since you are only interested in the respective residual that remains after the division by the factor of 5.
The last examples highlight the fact that by using this type of arithmetic, you can add a whole-number multiple of the module number (here 5) at any time, but the result will always be the same.
This pattern also works for multiplication.
An example:
4 mod5 * 2 mod5 = 8 mod5 = 3 mod5
You can also write:
9 mod5 * 7 mod5 = 63 mod5 = 3 mod5
since you can simply deduct 60, hence 5 * 12.
But you could also write:
9 mod5 * 7 mod5 = 4 mod5 * 2 mod5 = 8 mod5 = 3 mod5
because 4 corresponds with 9 and 2 corresponds with 7, if you examine only the residual after a division by 5.
Again, we see that it does not matter if we simply leave out the multiple of five.
Since this makes everything much simpler, we will do this before adding or multiplying numbers. This means that we only need to concern ourselves with numbers 0, 1, 2, 3, 4 when doing arithmetic modulo 5, as we can leave out all that is divisible by 5.
Three more examples:
Computers store letters as numbers. All the letters and symbols found on a computer keyboard are actually stored as numbers between 0 and 255.
As a result, it is possible to convert a message into a series of numbers. The method (or algorithm) used for this process will be described in the next section, which will introduce the method used for the encryption with GnuPG: the RSA algorithm. This algorithm converts a series of numbers (which can represent a message) into a different series of numbers (transformation) in such a way that the message is thereby encrypted. Using the correct method, the message is securely encoded and may only be decoded by the right recipient.
These are the principles behind the RSA algorithm:
You created two large prime numbers when you entered your passphrase for creating a certificate (they are described as p and q). Only you, or actually your computer, knows these two prime numbers and you must ensure they stay secret.
They are now used to create three additional numbers:
d = e-1 mod(p - 1)(q -1)
The first and second number are published -- your public key. Both are used to encrypt messages. The third number -- your private key -- must be kept secret. Afterwards, the two prime numbers (p und q) are no longer required.
When an encrypted message is received, it can be decrypted using the first (n) and third number (d). Only the receipient knows both parts of the key -- his public and private key. The rest of the world only knows the public key (n und e).
The trick of the RSA algorithm is that it makes it impossible to calculate the private key portion (d) from the public key portion (n and e) and hence decrypt the message because -- only the person with d is able to decrypt the message.
We will initially be using small numbers in order to show how the method works. However, in practice much larger multi-digit prime numbers are used.
Let's take prime numbers 7 and 11 and use them to encrypt numbers -- or letters, which is one and the same to the computer -- according to the RSA algorithm.
We will first be creating the public key
First, we deduct 1 from each of our prime numbers 7 und 11 (hence 7 - 1 and 11 - 1) and multiply the two resulting numbers to obtain 60: ( 7 - 1 ) * ( 11 - 1) = 60. 60 is our module number for the further calculation of the private key (however, not to be confused with the actual modulus 77).
Now we look for a number which, when multiplied with the public key, results in the number 1, when using module 60:
13 mod60 * ? mod60 = 1 mod60
The only number that fits this requirement is 37 because
13 mod60 * 37 mod60 = 481 mod60 = 1 mod60
37 is the only number that results in 1 when multiplied with 13, using module 60.
We now divide the message into a series of numbers between 0 and 76, i.e. 77 numbers, because both encryption and decryption use module 77 (the product obtained from the prime numbers 7 and 11).
Each one of these numbers is now multiplied with itself 13 times, as per modulo 77 arithmetics. Remember: 13 is our public key.
Let's take an example using the number 2 which is converted into 30, because 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 = 213 = 8192 = 30 mod77 .
Another example: 75 is converted into 47, because 75 is multiplied by itself 13 times and divided by 77, leaving the residual 47.
If you use this calculation for all numbers between 0 and 76 and insert the results into a table, it will look as follows:
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 1 | 30 | 38 | 53 | 26 | 62 | 35 | 50 | 58 |
| 10 | 10 | 11 | 12 | 41 | 49 | 64 | 37 | 73 | 46 | 61 |
| 20 | 69 | 21 | 22 | 23 | 52 | 60 | 75 | 48 | 7 | 57 |
| 30 | 72 | 3 | 32 | 33 | 34 | 63 | 71 | 9 | 59 | 18 |
| 40 | 68 | 6 | 14 | 43 | 44 | 45 | 74 | 5 | 20 | 70 |
| 50 | 29 | 2 | 17 | 25 | 54 | 55 | 56 | 8 | 16 | 31 |
| 60 | 4 | 40 | 13 | 28 | 36 | 65 | 66 | 67 | 19 | 27 |
| 70 | 42 | 15 | 51 | 24 | 39 | 47 | 76 |
Table 1
The left column shows multiples of tens, the upper row shows the
units.
To reverse the example above using the number 2, i.e. to decode the message, we multiply 30 (the converted 2) by itself 37 times (3037). The result is calculated using module number 77. Remember: 37 is the private key.
This repeated multiplication results in 2 mod77. The other example: the number 47 mod77 is decoded into the number 75mod77.
Table 2 shows the exact allocation of the 77 numbers between 0 and 76.
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 1 | 51 | 31 | 60 | 47 | 41 | 28 | 57 | 37 |
| 10 | 10 | 11 | 12 | 62 | 42 | 71 | 58 | 52 | 39 | 68 |
| 20 | 48 | 21 | 22 | 23 | 73 | 53 | 5 | 69 | 63 | 50 |
| 30 | 2 | 59 | 32 | 33 | 34 | 7 | 64 | 16 | 3 | 74 |
| 40 | 61 | 13 | 70 | 43 | 44 | 45 | 18 | 75 | 27 | 14 |
| 50 | 8 | 72 | 24 | 4 | 54 | 55 | 56 | 29 | 9 | 38 |
| 60 | 25 | 19 | 6 | 35 | 15 | 65 | 66 | 67 | 40 | 20 |
| 70 | 49 | 36 | 30 | 17 | 46 | 26 | 76 |
Table 2: Number transformation modulo 77, using the private key 37
In order to transform a number using Table
2, we use the same method as for
Table 1. An example: 60 is transformed
into the number in row 60 and column 0. Hence 60 is transformed to
25.
This is not surprising, as if we assume that using Table 1 for the conversion of 25 results in 60, it only stands to reason that we should obtain 25 for the transformation of 60 when using Table 2. In doing so we used the public key, 13, for the conversion (codification) of a number, and the private key 37 in order to reverse the process, i.e. decoding. We have used modulo 77 arithmetics both for the encryption and decryption process.
You have ...
The two prime numbers selected can be so large that it is impossible to decipher them by any publicly known product. This is the basis for the security of the RSA algorithm.
We have seen that the calculations can become quite complex, even when a simple example is used. In this case, the person who made the key public has published the numbers 77 and 13 as a public key. With this information, anyone can send this person an encrypted number of series of numbers using the method described above -- as in the example of Table 1. The intended recipient of the encrypted series of numbers can decode these using the number 77 and the private key 37.
Of course, a simple example such as this one does not guarantee a particularly secure encryption, as it is quite clear that 77 is the product of 7 and 11.
As a result, it would be fairly easy to crack the code of this simple example. The discerning reader will also have noticed that there are a whole series of numbers, such as the number 11 and its multiples (22, 33 etc) and neighbouring numbers convert into themselves.
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 1 | 51 | 31 | 60 | 47 | 41 | 28 | 57 | 37 |
| 10 | 10 | 11 | 12 | 62 | 42 | 71 | 58 | 52 | 39 | 68 |
| 20 | 48 | 21 | 22 | 23 | 73 | 53 | 5 | 69 | 63 | 50 |
| 30 | 2 | 59 | 32 | 33 | 34 | 7 | 64 | 16 | 3 | 74 |
| 40 | 61 | 13 | 70 | 43 | 44 | 45 | 18 | 75 | 27 | 14 |
| 50 | 8 | 72 | 24 | 4 | 54 | 55 | 56 | 29 | 9 | 38 |
| 60 | 25 | 19 | 6 | 35 | 15 | 65 | 66 | 67 | 40 | 20 |
| 70 | 49 | 36 | 30 | 17 | 46 | 26 | 76 |
Table 3
This appears to be a further weakness of this encryption method: one
could assume that this would limit the security of the algorithm.
However, imagine that the product of two large, randomly selected,
prime numbers results in the following:
114,381,625,757,888,867,669,235,779,976,146,612,010, 218,296,721,242,362,562,561,842,935,706,935,245,733, 897,830,597,123,563,958,705,058,989,075,147,599,290, 026,879,543,541
In this example it is no longer possible to discern the starting prime numbers. As a result it is very difficult to determine the private key using the public key. Even the fastest computers in the world would have great difficulty in calculating the two prime numbers. Hence - all that is required is to select prime numbers that are big enough to deter all known methods for determination in practice. Furthermore, the proportion of number which are converted into themselves - as shown in above in 1 and2, continuously decreases as the prime numbers get bigger.
Of the prime numbers in the range which we use for encryption in practice, this portion is to small that the RSA algorithm is in no way restricted by it.
The larger the prime numbers, the more secure the encryption. A normal PC has no difficulty in obtaining the product from the two large prime numbers. However, no computer in the world can derive the original prime numbers from this product - at least not in the foreseeable future.
In order to understand how messages are encrypted, one should know how a computer stores numbers and above all, how they can be represented in many different number bases.
For this purpose, let us first look at the power of numbers.
Two to the power of one, displayed as 21 = 2;
Two to the power of three, displayed as 23 = 2 * 2 * 2 = 8;
Two to the power of 10, displayed as 210 = 2*2*2*2*2*2*2*2*2*2 = 1024.
Each number to the power of zero equals 1, e.g. 20 = 1 and 50 = 1. Put more generally, it means that a number is multiplied by itself as many times as indicated by the number of the power.
The concept of a number basis can also be seen in the example of an
odometer in a vehicle: the right wheel counts to the next number after
each kilometre, according to the known sequence:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, ...
Each time the right wheel reaches 0, the wheel on the left counts up by a level. And each time when this second wheel reaches 0, the wheel to its left also goes up by one ...and so on.

The right wheel counts single kilometres. When it marks an 8, it means 8 kilomtres. The wheel to the left shows every full ten kilometres: a 5 means 50 kilometres. This is followed by the hundred indicator: a 7 means 700 kilometres.
We use the same principles to illustrate regular numbers with the digits 0 to 9.
For example, "578" means 5 * 100 + 7 * 10 + 8, which corresponds to 578.
Here we have the "5" which stands for five hundred, "7" for seventy and "8" for eight. In this case the base is 10, one which is quite familiar to us.
Hence the right digit represents the 'units' of a particular number (i.e. it is multiplied with 1), the digit to the left represents the 'tens' (i.e. multiplied by 10), the next for 'hundreds' (i.e. multiplied by 100) and so on. Since we usually represent numbers using a basis of 10, we do not need to separately indicate the base. On a more formal level, this would be indicated as 5510 for the number 55, whereby the base is represented by the subscript number.
If we are not using a base of 10, we have to use a corresponding subscript to indicate the relevant number.
Assume that, instead of using the digits 0 to 8, the odometer indicator only included digits 0 to 7. The right wheel would thus continue to count up one level after each kilometres, with the resulting number series looking as follows:
0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, ...
For example, your three-digit odometer using the base 8 would represent the following number:
356
The 6 on the right wheel counts single kilometres, hence 6*80=6
kilometres.
The 5 on the wheel beside it stands for 5 * 81, hence 40
kilometres.
The 3 left of that stands for each 64 kilometres per revolution, in
this example 3 * 82 kilometres.
This is how calculating numbers with basis of 8 works. An example:
728 represents 7 * 81 + 2 * 80 = 58.
In this illustration, the "2" from 72 stands for 2, but the "7"
stands for 7 * 8.
Larger numbers are gradually assembled in the same way, so that
4538 actually reprsents 4 * 64 + 5 * 8 + 3, which results in
29910t.
For 4538, the "3" stands for 3, the "5" for 5 * 8 and the
"4" for 4 * 64, whereby the "64" is in turn derived from 8 *
8.
In the example above digits are multiplied by ascending powers of 8, from left to right. The right digit is multiplied with 80 (i.e. 1), while the the digit to the left is multiplied wiht 81 (i.e. 8), and the one to the left with 82 (i.e. 64), and so on.
When representing numbers with a base of 10, there is no higher digit
than 9 (i.e. 10 minus 1). Hence there is no digit which represents 10
or a higher number. In order to represent 10, we need two digits with
which to write "10".
So we only have digits 0 to 9.
Much the same applies when calculating with the base number 8: the
only available digits are 0 to 7. If we wish to represent a number
higher than seven using this base, we must again use two digits. For
example, 910 is 118, 7310 is 1118.
Computers stores numbers as a series of zeros and ones. This is called the binary system or arithmetics using the base number 2, because we are only using the digits 0 and 1. Imagine counting kilometres with an odometer whose wheel only has two digits: 0 and 1. Hence, using the binary system, the number 101012, for example, would look as follows
1*24+0*23+1*22+0*21+1*20 = 1 * 16 + 0 * 8 + 1 * 4 + 0 * 2 + 1 = 21
Groups of eight binary digits are also used in computer technology - the well known "byte". A byte can consist of values anywhere from 0 - represented as byte 000000002 -- and 255 -- represented as byte 111111112. A byte therefore represents the number to the base of 28 = 256.
Two more examples:
101010102 = 170
000001012 = 5
Since the computer stores letters, digits and symbols as bytes, let us see the role played by the representation to the base of 256.
Let's take the syllable "un". The computer stores "u" as 117, and the "n" as 110.
These number values are standard for all computers and are called ASCII code.
You can also represent the syllable "un" with the following number:
117 * 28*1 + 110 * 28*0 = 117 * 256 + 110 = 30062
Accordingly, the letter sequence "und" would be represented with the number
117 * 28*2 + 110 * 28*1 + 100 * 28*0 = 117 * 65536 + 110 * 256 + 100 = 7695972
since "d" is represented by 100.
We have therefore internally represented numbers and symbols which are available on a computer keyboard as normal numbers using the base of 10 by numbers to the base of 28 = 256.
Accordingly we are able to turn every message into a big number. A long message leads to an enormously large number, which we wish to encrypt with the RSA algorithm.
However, we must ensure that the number into which the message is
encrypted does not become larger than the product of the prime numbers
(modulus), otherwise it creates problems, as we will see below.
Since the next process is comprised a number of steps, let's first
summarize and then examine the individual steps in turn:
And now in detail:
Assuming we limit the messages to the four letters a, b, c und d, using this -- very simple -- example we could represent the four letters by the number values 0, 1, 2 and 3, and hence have
a = 0, b = 1, c = 2 und d = 3
Now encrypt the message aba, cad, aca. Encode the message
using prime numbers 7 and 11, with the public
key 77 und 13 and associated private key 37. You area already
familiar with this example from an earlier chapter: You used it to
construct the tables 1 and
2.
Because you are using four letters for the message, calculate using a basis of 4. For a modulo 77 calculation, you have to break down the message into pieces of three digits each, because the largest three-digit number using a basis of 4 is 3334. Using a basis of 10, this number has a value of 63.
If instead you were to divide the message into pieces of four characters each, 33334 would exceed the value of 7610 and would result in unwanted ambiguity.
As a result, the message of three-digit pieces would result in
aba, cad, aca
Now assign your number values to the characters and do not forget that the pieces represent three-digit numbers using a basis of 4.
Since you are representing the letters with the numbers a = 0, b = 1, c = 2, d = 3, the resulting message will look as follows:
0104, 2034, 0204
Using a basis of 10, this message will be represented by the number sequence 4, 35, 8. Why? For example, take the middle part 2034:
|
3 * 4^0, | also 3 * 1, | also 3. |
| 0 * 4^1, | also 0 * 4, | also 0. |
| 2 * 4^2, | also 2 * 16, | also 32. |
To encrypt the message, you now use the aforementioned
table 1. The message now turns into
the number sequence 53, 63, 50 (basis of 10).
Therefore we reverse the process and transform the number sequence 53, 63, 50 using Table 2 to obtain the sequence 4, 35, 8, which precisely corresponds with the original message.
Using Tables 1 and2 you can also encrypt messages using the private key (e.g. first use Table 2 and then decode with the public key (i.e. Table 1) and thus restore your original number). This allows the owner of the private key to encrypt messages using the RSA algorithm, and it proves that the messages can only come from him.
.... while this process is complicated in its details, the principle on the other hand is fairly easy to understand. After all, you should not just trust a method but also - at least on the basis of understanding the approach behind it - be able to see behind its mode of operation. Many of the other details can easily be found in other books (z.B.: R. Wobst, "Abenteuer Kryptologie") or on the Internet.
In any case, now you know: if someone should ever attempt to crack your encrypted e-mails, the process will keep them busy for such a long time that they will lose all interest in actually reading your messages......
© 31. August 2010, v3.0.0-beta1 (last minor changes from 21. September 2010)
The Gpg4win Compendium is filed under the
GNU Free Documentation License v1.2.
 |
 |
 |
 | 25 GnuPG and the mystery of large numbers
| Contents |
 |